電磁誘導と微積分

綾瀬個別指導学院（講師編）です。

今回は、電磁誘導と微積分についてです。

一様な磁場内でコイルを一定の速さで回転させたときに発生する誘導起電力は、微積分を用いて容易に求めることができます。


まず、1巻きのコイルを貫く磁束Φが時間Δtの間にΔΦだけ変化するときの誘導起電力Vは
　　　　　　　V=-ΔΦ/Δt　（ファラデーの電磁誘導の法則）
です。この式は、誘導起電力Vが磁束Φの時間tに対する平均変化率であることを表しています。

したがって、瞬間の変化率は
　　　　　　　　　　V=-dΦ/dt
のように、Φをtで微分することによって得ることができます。


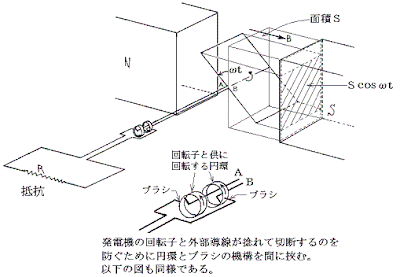
上図のコイルの辺の長さをl, 2rとすると、コイルの面積は2rlですから、コイルを貫く磁束は
　　　　　　　　　　Φ=B×2rlcosωt
となります。

したがって、誘導起電力は
　　　　　　V=-dΦ/dt=2Brlωsinωt=V0sinωt
と求められます。（ただし、V0=2Brlω）

ＨＰはこちらから→　クリック

資料請求・お問い合わせはこちら→クリック

綾瀬　塾
綾瀬２教室
都立受験に強い
万全の定期テスト対策　　入試対策　
綾瀬駅西口徒歩１分
地域密着　綾瀬個別指導学院
綾瀬　塾　評判